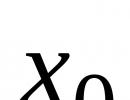Limita funkcie – definície, vety a vlastnosti. Limit postupnosti a funkcie. Limitné vety Určenie limity funkcie podľa Heineho

Limita funkcie v bode a v

Limita funkcie je hlavným aparátom matematickej analýzy. S jeho pomocou sa následne určí spojitosť funkcie, derivácia, integrál a súčet radu.

Nech je funkcia y=f(X)definované v niektorom okolí bodu , snáď okrem samotného bodu .

Sformulujme dve ekvivalentné definície limity funkcie v bode.

Definícia 1 (v „jazyku sekvencií“ alebo podľa Heineho). číslo b volal limit funkcie r=f(X) v bode (alebo kedy
), ak pre akúkoľvek sekvenciu platných hodnôt argumentov

konvergujúce k (tie.
), postupnosť zodpovedajúcich funkčných hodnôt
konverguje k číslu b(tie.
).

V tomto prípade píšu
alebo
pri
. Geometrický význam limity funkcie:
znamená, že pre všetky body X, dostatočne blízko k bodu , zodpovedajúce hodnoty funkcie sa od čísla líšia tak málo, ako si želáte b.

Definícia 2 (v jazyku“, alebo podľa Cauchyho). číslo b volal limit funkcie r=f(X) v bode (alebo kedy
), ak pre akékoľvek kladné číslo  existuje kladné číslo  také, že pre všetky
uspokojenie nerovnosti
, nerovnosť platí
.

Zapíšte si
.

Táto definícia sa dá stručne napísať takto:

Všimni si
dá sa napísať aj takto
.

G geometrický význam limity funkcie:
, ak pre nejaké okolie bodu b existuje také okolie bodu to je pre každého
z tohto okolia zodpovedajúce hodnoty funkcie f (X) ležia v okolí bodu b. Inými slovami, body na grafe funkcie r = f (X) ležať vo vnútri pásu šírky 2 ohraničeného priamkami pri = b + , pri = b  (Obrázok 17). Je zrejmé, že hodnota  závisí od výberu , takže píšu  = ().

Príklad Dokáž to

Riešenie . Zoberme si ľubovoľné   0 a nájdime  = ()  0 také, že pre všetky X
, nerovnosť platí
. Keďže od

tie.
, potom brať , to vidíme u všetkých X, uspokojujúce nerovnosť
, nerovnosť platí
. teda

Príklad Dokážte, že ak f (X) = s, To
.

Riešenie . Pre
môžeš si to vziať
. Potom o

máme . teda
.

Pri definovaní limity funkcie
Verí sa, že X usiluje o akýmkoľvek spôsobom: zostáva menej ako (naľavo od ), väčší než (vpravo od ), alebo kolísanie okolo bodu .

Existujú prípady, keď metóda aproximácie argumentu X Komu výrazne ovplyvňuje hodnotu limitu funkcie. Preto sa zavádzajú koncepty jednostranných limitov.

Definícia. číslo volal limit funkcie r=f(X) vľavo v bode , ak pre ľubovoľné číslo   0 existuje číslo  = ()  0 také, že pre
, nerovnosť platí
.

Limit vľavo je napísaný nasledovne
alebo krátko
(Dirichletov zápis) (Obrázok 18).

Definované podobne limit funkcie vpravo , napíšme to pomocou symbolov:

Stručne je označená hranica vpravo
.

P Zavolajú sa limity funkcie vľavo a vpravo jednosmerné limity . Samozrejme, ak existuje
, potom existujú obe jednostranné limity a
.

Platí to aj naopak: ak existujú obe limity
A
a sú si rovní, potom je tu hranica
A .

Ak
, To
neexistuje.

Definícia. Nechajte funkciu r=f(X) je definovaný v intervale
. číslo b volal limit funkcie r=f(X) pri X , ak pre akékoľvek číslo   0 existuje také číslo M = M()  0, čo pre všetkých X, uspokojujúce nerovnosť
nerovnosť platí
. Stručne možno túto definíciu napísať takto:

E ak X +, potom napíšu
, Ak X , potom píšu
, Ak
=
, potom sa zvyčajne označuje ich všeobecný význam
.

Geometrický význam tejto definície je nasledovný: pre
, že o
A
zodpovedajúce funkčné hodnoty r=f(X) spadajú do okolia bodu b, t.j. body grafu ležia v páse šírom 2, ohraničenom priamkami
A
(Obrázok 19).

Funkcia y = f (X) je zákon (pravidlo), podľa ktorého každý prvok x množiny X je spojený s jedným a len jedným prvkom y množiny Y.

Prvok x ∈ X volal argument funkcie alebo nezávislá premenná.
Prvok y ∈ Y volal funkčná hodnota alebo závislá premenná.

Množina X sa nazýva doména funkcie.
Súbor prvkov y ∈ Y, ktoré majú predobrazy v množine X, sa nazýva oblasť alebo súbor funkčných hodnôt.

Volá sa skutočná funkcia obmedzené zhora (zdola), ak existuje číslo M také, že nerovnosť platí pre všetkých:
.
Zavolá sa funkcia čísla obmedzené, ak existuje číslo M také, že pre všetky:
.

Horný okraj alebo presná horná hranica Skutočná funkcia sa nazýva najmenšie číslo, ktoré obmedzuje rozsah jej hodnôt zhora. To znamená, že toto je číslo s, pre ktoré pre každého a pre kohokoľvek existuje argument, ktorého funkčná hodnota presahuje s′: .
Horná hranica funkcie môže byť označená takto:
.

Respektíve spodný okraj alebo presná spodná hranica Skutočná funkcia sa nazýva najväčšie číslo, ktoré obmedzuje rozsah jej hodnôt zdola. To znamená, že toto je číslo i, pre ktoré pre každého a pre kohokoľvek existuje argument, ktorého funkčná hodnota je menšia ako i′: .
Infimum funkcie možno označiť takto:
.

Určenie limity funkcie

Určenie limity funkcie podľa Cauchyho

Konečné limity funkcie v koncových bodoch

Nech je funkcia definovaná v nejakom okolí koncového bodu, možno s výnimkou samotného bodu. v bode if for any existuje taká vec, v závislosti od , že pre všetky x pre ktoré platí nerovnosť
.
Limita funkcie je označená takto:
.
Alebo na .

Pomocou logických symbolov existencie a univerzálnosti možno definíciu limity funkcie napísať takto:
.

Jednostranné limity.
Ľavý limit v bode (ľavý limit):
.
Pravý limit v bode (pravý limit):
.
Ľavý a pravý limit sa často označujú takto:
; .

Konečné limity funkcie v bodoch v nekonečne

Limity v bodoch v nekonečne sa určujú podobným spôsobom.
.
.
.
Často sa označujú ako:
; ; .

Použitie konceptu okolia bodu

Ak zavedieme koncept prepichnutého okolia bodu, potom môžeme dať jednotnú definíciu konečnej limity funkcie v konečných a nekonečne vzdialených bodoch:
.
Tu pre koncové body
; ;
.
Akékoľvek okolie bodov v nekonečne je prepichnuté:
; ; .

Nekonečné funkčné limity

Definícia
Nech je funkcia definovaná v nejakom punktovanom okolí bodu (konečného alebo v nekonečne). Limita funkcie f (X) ako x → x 0 rovná sa nekonečnu, ak pre ľubovoľne veľké číslo M > 0 , existuje číslo δ M > 0 , v závislosti od M, že pre všetky x patriace do prepichnutého δ M - okolia bodu: platí nerovnosť:
.
Nekonečná hranica je označená takto:
.
Alebo na .

Pomocou logických symbolov existencie a univerzálnosti možno definíciu nekonečnej limity funkcie napísať takto:
.

Môžete tiež zaviesť definície nekonečných limitov určitých znakov rovných a :
.
.

Univerzálna definícia limity funkcie

Pomocou konceptu okolia bodu môžeme poskytnúť univerzálnu definíciu konečnej a nekonečnej limity funkcie, použiteľnú pre konečné (obojstranné a jednostranné) aj nekonečne vzdialené body:
.

Určenie limity funkcie podľa Heineho

Nech je funkcia definovaná na nejakej množine X:.
Číslo a sa nazýva limita funkcie v bode:
,
ak pre akúkoľvek postupnosť konvergujúcu k x 0 :
,
ktorých prvky patria do množiny X: ,
.

Napíšme túto definíciu pomocou logických symbolov existencie a univerzálnosti:
.

Ak vezmeme ľavostranné okolie bodu x ako množinu X 0 , potom získame definíciu ľavej limity. Ak je pravotočivý, dostaneme definíciu správnej hranice. Ak zoberieme okolie bodu v nekonečne ako množinu X, dostaneme definíciu limity funkcie v nekonečne.

Veta
Cauchyho a Heineho definície limity funkcie sú ekvivalentné.
Dôkaz

Vlastnosti a vety limity funkcie

Ďalej predpokladáme, že uvažované funkcie sú definované v zodpovedajúcom okolí bodu, ktorým je konečné číslo alebo jeden zo symbolov: . Môže to byť aj jednostranný hraničný bod, teda mať tvar alebo . Okolie je obojstranné pre obojstranný limit a jednostranné pre jednostranný limit.

Základné vlastnosti

Ak hodnoty funkcie f (X) zmeniť (alebo urobiť nedefinovaným) konečný počet bodov x 1, x 2, x 3, ... x n, potom táto zmena neovplyvní existenciu a hodnotu limity funkcie v ľubovoľnom bode x 0 .

Ak existuje konečná limita, potom existuje prepichnuté okolie bodu x 0 , na ktorom je funkcia f (X) obmedzené:
.

Nech má funkcia v bode x 0 konečná nenulová hranica:
.
Potom pre ľubovoľné číslo c z intervalu existuje takéto prepichnuté okolie bodu x 0 , za čo ,
, Ak ;
, Ak .

Ak je na niektorom prepichnutom okolí bodu , konštanta, potom .

Ak existujú konečné limity a a na nejakom prerazenom okolí bodu x 0
,
To .

Ak , a na niektorom okolí bodu
,
To .
Najmä ak je v niektorom susedstve bodu
,
potom ak , potom a ;
ak , potom a .

Ak na nejakom prerazenom okolí bodu x 0 :
,
a existujú konečné (alebo nekonečné určitého znamienka) rovnaké limity:
, To
.

Dôkazy o hlavných vlastnostiach sú uvedené na stránke
"Základné vlastnosti limity funkcie."

Aritmetické vlastnosti limity funkcie

Nech sú funkcie a definované v niektorom prepichnutom okolí bodu. A nech existujú konečné limity:
A .
A nech C je konštanta, teda dané číslo. Potom
;
;
;
, Ak .

Ak potom.

Dôkazy aritmetických vlastností sú uvedené na stránke
"Aritmetické vlastnosti limity funkcie".

Cauchyho kritérium pre existenciu limity funkcie

Veta
Aby bola funkcia definovaná na nejakom punktovanom okolí konečného alebo v nekonečnom bode x 0 , mal v tomto bode konečnú limitu, je potrebné a postačujúce, aby pre akékoľvek ε > 0 tam bolo také prepichnuté okolie bodu x 0 , že pre všetky body a z tohto okolia platí nasledujúca nerovnosť:
.

Limita komplexnej funkcie

Veta o limite komplexnej funkcie
Nech má funkcia limit a mapuje punktované okolie bodu na punktované okolie bodu. Nech je funkcia definovaná na tomto okolí a má naň limit.
Tu sú konečné alebo nekonečne vzdialené body: . Okolie a im zodpovedajúce limity môžu byť obojstranné alebo jednostranné.
Potom existuje limita komplexnej funkcie a rovná sa:
.

Limitná veta komplexnej funkcie sa aplikuje, keď funkcia nie je definovaná v bode alebo má hodnotu odlišnú od limity. Ak chcete použiť túto vetu, musí existovať prepichnuté okolie bodu, kde množina hodnôt funkcie neobsahuje bod:
.

Ak je funkcia spojitá v bode , znamienko limitu možno použiť na argument spojitej funkcie:
.
Nasleduje veta zodpovedajúca tomuto prípadu.

Veta o limite spojitej funkcie funkcie
Nech existuje limita funkcie g (t) ako t → t 0 a rovná sa x 0 :
.
Tu je bod t 0 môže byť konečná alebo nekonečne vzdialená: .
A nechajte funkciu f (X) je spojitá v bode x 0 .
Potom existuje limita komplexnej funkcie f (g(t)), a rovná sa f (x0):
.

Dôkazy teorémov sú uvedené na stránke
„Limita a kontinuita komplexnej funkcie“.

Nekonečne malé a nekonečne veľké funkcie

Infinitezimálne funkcie

Definícia
O funkcii sa hovorí, že je nekonečne malá, ak
.

Súčet, rozdiel a súčin konečného počtu nekonečne malých funkcií v je nekonečne malá funkcia v .

Súčin funkcie ohraničenej na nejakom punktovanom okolí bodu , k infinitezimálnemu at je nekonečne malá funkcia v .

Na to, aby funkcia mala konečnú limitu, je potrebné a postačujúce, že
,
kde je infinitezimálna funkcia v .

"Vlastnosti nekonečne malých funkcií".

Nekonečne veľké funkcie

Definícia
O funkcii sa hovorí, že je nekonečne veľká, ak
.

Súčet alebo rozdiel obmedzenej funkcie na nejakom prepichnutom okolí bodu a nekonečne veľkej funkcie v je nekonečne veľká funkcia v bode .

Ak je funkcia nekonečne veľká pre a funkcia je ohraničená nejakým prepichnutým okolím bodu, potom
.

Ak funkcia na nejakom prepichnutom okolí bodu spĺňa nerovnosť:
,
a funkcia je nekonečne malá pri:
, a (na niektorom prepichnutom okolí bodu), potom
.

Dôkazy vlastností sú uvedené v časti
"Vlastnosti nekonečne veľkých funkcií".

Vzťah medzi nekonečne veľkými a nekonečne malými funkciami

Z dvoch predchádzajúcich vlastností vyplýva súvislosť medzi nekonečne veľkými a nekonečne malými funkciami.

Ak je funkcia nekonečne veľká v , potom je funkcia nekonečne malá v .

Ak je funkcia nekonečne malá pre , a , potom je funkcia nekonečne veľká pre .

Vzťah medzi nekonečne malou a nekonečne veľkou funkciou možno vyjadriť symbolicky:
, .

Ak má infinitezimálna funkcia určité znamienko v , to znamená, že je kladná (alebo záporná) v niektorom punktovanom okolí bodu , potom túto skutočnosť možno vyjadriť takto:
.
Rovnakým spôsobom, ak má nekonečne veľká funkcia určité znamienko v , potom píšu:
.

Potom možno symbolickú súvislosť medzi nekonečne malými a nekonečne veľkými funkciami doplniť nasledujúcimi vzťahmi:
, ,
, .

Ďalšie vzorce týkajúce sa symbolov nekonečna nájdete na stránke
"Body v nekonečne a ich vlastnosti."

Limity monotónnych funkcií

Definícia
Zavolá sa funkcia definovaná na nejakej množine reálnych čísel X prísne zvyšovať, ak pre všetky platí nasledujúca nerovnosť:
.
V súlade s tým pre prísne klesá funkcia platí nasledujúca nerovnosť:
.
Pre neklesajúci:
.
Pre nezväčšujúce sa:
.

Z toho vyplýva, že striktne rastúca funkcia je aj neklesajúca. Striktne klesajúca funkcia je tiež nerastúca.

Funkcia sa volá monotónna, ak je neklesajúca alebo nezvyšujúca sa.

Veta
Nech funkcia neklesá na intervale kde .
Ak je hore ohraničený číslom M: potom existuje konečná limita. Ak to nie je obmedzené zhora, potom .
Ak je zdola ohraničená číslom m: tak existuje konečná hranica. Ak nie je obmedzený zdola, potom .

Ak sú body a a b v nekonečne, potom vo výrazoch medzné znamienka znamenajú, že .
Táto veta môže byť formulovaná kompaktnejšie.

Nech funkcia neklesá na intervale kde . Potom existujú jednostranné limity v bodoch a a b:
;
.

Podobná veta pre nerastúcu funkciu.

Nech sa funkcia nezvýši na intervale kde . Potom sú tu jednostranné limity:
;
.

Dôkaz vety je uvedený na stránke
"Limity monotónnych funkcií".

Referencie:
L.D. Kudrjavcev. Kurz matematickej analýzy. Zväzok 1. Moskva, 2003.
CM. Nikolského. Kurz matematickej analýzy. Zväzok 1. Moskva, 1983.

Konštantné číslo A volal limit sekvencie(x n ), ak pre ľubovoľne malé kladné čísloε > 0 existuje číslo N, ktoré má všetky hodnoty x n, pre ktoré n>N vyhovujú nerovnici

|x n - a|< ε. (6.1)

Zapíšte si to takto: alebo x n → a.

Nerovnosť (6.1) je ekvivalentná dvojitej nerovnosti

a- ε< x n < a + ε, (6.2)

čo znamená, že body x n, začínajúc od nejakého čísla n>N, ležia vo vnútri intervalu (a-ε, a+ ε ), t.j. spadnúť do akéhokoľvek maléhoε - susedstvo bodu A.

Zavolá sa postupnosť s limitom konvergentné, inak - divergentný.

Pojem limita funkcie je zovšeobecnením konceptu limity postupnosti, keďže limitu postupnosti možno považovať za limitu funkcie x n = f(n) celočíselného argumentu. n.

Nech je daná funkcia f(x) a nech a - limitný bod doména definície tejto funkcie D(f), t.j. taký bod, ktorého každé okolie obsahuje body množiny D(f) iné ako a. Bodka a môže alebo nemusí patriť do množiny D(f).

Definícia 1.Konštanta číslo A sa nazýva limit funkcie f(x) pri x→a, ak pre ľubovoľnú postupnosť (x n ) hodnôt argumentov má tendenciu A, zodpovedajúce postupnosti (f(x n)) majú rovnakú limitu A.

Táto definícia sa nazýva definovaním limity funkcie podľa Heineho, alebo " v sekvenčnom jazyku”.

Definícia 2. Konštanta číslo A sa nazýva limit funkcie f(x) pri x→a, ak zadaním ľubovoľne malého kladného čísla ε, možno nájsť také δ>0 (v závislosti od ε), ktorý je pre každého X, ležiaci vε-okolia čísla A, t.j. Pre X, uspokojujúce nerovnosť
0 < x-a< ε , hodnoty funkcie f(x) budú ležať vε-okolie čísla A, t.j.|f(x)-A|< ε.

Táto definícia sa nazýva definovaním limity funkcie podľa Cauchyho, alebo “v jazyku ε - δ “.

Definície 1 a 2 sú ekvivalentné. Ak funkcia f(x) ako x →má limit, rovná sa A, toto sa píše v tvare

. (6.3)

V prípade, že postupnosť (f(x n)) rastie (alebo klesá) bez obmedzenia pre akúkoľvek metódu aproximácie X na svoj limit A, potom povieme, že funkcia f(x) má nekonečný limit, a napíšte to v tvare:

Volá sa premenná (t. j. postupnosť alebo funkcia), ktorej limita je nula nekonečne malý.

Volá sa premenná, ktorej limita sa rovná nekonečnu nekonečne veľký.

Na nájdenie limity v praxi sa používajú nasledujúce vety.

Veta 1 . Ak existuje každý limit

(6.4)

(6.5)

(6.6)

Komentujte. Výrazy ako 0/0, ∞/∞, ∞-∞ , 0*∞ , - sú neisté, napríklad pomer dvoch nekonečne malých alebo nekonečne veľkých veličín a nájdenie limitu tohto typu sa nazýva „odkrývanie neistôt“.

Veta 2. (6.7)

tie. možno ísť na limit založený na mocnine s konštantným exponentom, najmä ;

(6.8)

(6.9)

Veta 3.

(6.10)

(6.11)

Kde e » 2.7 - základ prirodzeného logaritmu. Vzorce (6.10) a (6.11) sa nazývajú prvé úžasná hranica a druhý pozoruhodný limit.

Dôsledky vzorca (6.11) sa používajú aj v praxi:

(6.12)

(6.13)

(6.14)

najmä limit,

Ak x → a a zároveň x > a, potom napíšte x→a + 0. Ak je konkrétne a = 0, potom namiesto symbolu 0+0 napíšte +0. Podobne, ak x→a a zároveň x a-0. čísla a podľa toho sa volajú pravý limit A ľavý limit funkcie f(x) v bode A. Aby existovala limita funkcie f(x) ako x→a je potrebné a postačujúce na to . Zavolá sa funkcia f(x). nepretržitý v bode x 0 ak limit

. (6.15)

Podmienku (6.15) možno prepísať ako:

,

to znamená, že prechod k limite pod znamienkom funkcie je možný, ak je v danom bode spojitá.

Ak je porušená rovnosť (6.15), hovoríme to pri x = xo funkciu f(x) Má medzera Uvažujme funkciu y = 1/x. Definičnou doménou tejto funkcie je množina R, okrem x = 0. Bod x = 0 je limitným bodom množiny D(f), keďže v ktoromkoľvek jej okolí, t.j. v akomkoľvek otvorenom intervale obsahujúcom bod 0 sú body z D(f), ale on sám do tejto množiny nepatrí. Hodnota f(x o)= f(0) nie je definovaná, takže v bode x o = 0 má funkcia diskontinuitu.

Zavolá sa funkcia f(x). súvislá vpravo v bode x o ako limit

,

A súvislá vľavo v bode x o, ak je limit

.

Spojitosť funkcie v bode xo je ekvivalentná jeho kontinuite v tomto bode vpravo aj vľavo.

Aby bola funkcia spojitá v bode xo, napríklad vpravo je potrebné, aby po prvé existovala konečná limita a po druhé, aby sa táto limita rovnala f(x o). Ak teda nie je splnená aspoň jedna z týchto dvoch podmienok, funkcia bude mať diskontinuitu.

1. Ak limita existuje a nerovná sa f(x o), potom to hovoria funkciu f(x) v bode x o má prasknutie prvého druhu, alebo skok.

2. Ak je limit+∞ alebo -∞ alebo neexistuje, potom hovoria, že v bod xo funkcia má diskontinuitu druhý druh.

Napríklad funkcia y = detská postieľka x na x→ +0 má limit rovný +∞, čo znamená, že v bode x=0 má diskontinuitu druhého druhu. Funkcia y = E(x) (celočíselná časť X) v bodoch s celými úsečkami má diskontinuity prvého druhu alebo skoky.

Zavolá sa funkcia, ktorá je spojitá v každom bode intervalu nepretržitý V . Spojitá funkcia je reprezentovaná plnou krivkou.

Mnohé problémy spojené s neustálym rastom nejakej veličiny vedú k druhej pozoruhodnej hranici. Medzi takéto úlohy patrí napríklad: rast ložísk podľa zákona zloženého úročenia, rast populácie krajiny, rozpad rádioaktívnych látok, premnoženie baktérií atď.

Uvažujme príklad Ya. I. Perelmana, poskytujúci výklad čísla e v probléme zloženého úroku. číslo e existuje limit . V sporiteľniach sa k fixnému kapitálu každoročne pridávajú úroky. Ak sa pristúpenie uskutočňuje častejšie, potom kapitál rastie rýchlejšie, pretože väčšia suma sa podieľa na tvorbe úrokov. Vezmime si čisto teoretický, veľmi zjednodušený príklad. Nech je v banke uložených 100 denárov. Jednotky na základe 100 % ročne. Ak sa úrokové peniaze pridajú k fixnému kapitálu až po roku, potom do tohto obdobia 100 den. Jednotky sa zmení na 200 peňažných jednotiek. Teraz sa pozrime, na čo sa 100 denize zmení. jednotiek, ak sa k fixnému kapitálu každých šesť mesiacov pridávajú úroky. Po šiestich mesiacoch 100 den. Jednotky narastie na 100× 1,5 = 150 a po ďalších šiestich mesiacoch - na 150× 1,5 = 225 (den. jednotky). Ak sa pristúpenie robí každú 1/3 roka, tak po roku 100 den. Jednotky sa zmení na 100× (1 + 1/3) 3 " 237 (den. jednotky). Zvýšime podmienky pre pridávanie úrokových peňazí na 0,1 roka, na 0,01 roka, na 0,001 roka atď. Potom zo 100 den. Jednotky po roku to bude:

100 × (1 + 1/10) 10 » 259 (den. jednotky),

100 × (1+1/100) 100 » 270 (den. jednotky),

100 × (1+1/1000) 1000 » 271 (den. jednotky).

Pri neobmedzenom znížení podmienok pre pripočítavanie úroku akumulovaný kapitál nerastie donekonečna, ale približuje sa k určitej hranici rovnajúcej sa približne 271. Kapitál uložený vo výške 100 % ročne sa nemôže zvýšiť viac ako 2,71-násobne, aj keď naakumulovaný úrok boli pridané do hlavného mesta každú sekundu, pretože limit

Príklad 3.1.Pomocou definície limity číselnej postupnosti dokážte, že postupnosť x n =(n-1)/n má limitu rovnajúcu sa 1.

Riešenie.Musíme to dokázať, nech sa deje čokoľvekε > 0, nech vezmeme čokoľvek, pre to existuje prirodzené číslo N také, že pre všetky n N platí nerovnosť|x n -1|< ε.

Vezmime ľubovoľné e > 0. Keďže ; x n -1 =(n+1)/n - 1= 1/n, potom na nájdenie N stačí vyriešiť nerovnosť 1/n< e. Preto n>1/e a preto N možno brať ako celú časť 1/ e, N = E(l/e ). Tým sme dokázali, že limit .

Príklad 3.2 . Nájdite limitu postupnosti danej spoločným členom .

Riešenie.Aplikujme limitu vety o súčte a nájdime limitu každého člena. Keď n→ ∞ Čitateľ a menovateľ každého člena majú tendenciu k nekonečnu a nemôžeme priamo použiť vetu o kvocientovej limite. Preto sa najprv transformujeme x n, delením čitateľa a menovateľa prvého členu o n 2, a druhý na n. Potom použitím limity kvocientu a limity vety o súčte zistíme:

.

Príklad 3.3. . Nájsť .

Riešenie. .

Tu sme použili vetu o limite stupňa: limita stupňa sa rovná stupňu limity základne.

Príklad 3.4 . Nájsť ( ).

Riešenie.Nie je možné použiť vetu o limite rozdielu, pretože máme neurčitosť tvaru ∞-∞ . Transformujme všeobecný výrazový vzorec:

.

Príklad 3.5 . Je daná funkcia f(x)=2 1/x. Dokážte, že neexistuje žiadny limit.

Riešenie.Použime definíciu 1 limity funkcie cez postupnosť. Zoberme si postupnosť ( x n ) konvergujúcu k 0, t.j. Ukážme, že hodnota f(x n)= sa pre rôzne postupnosti správa odlišne. Nech x n = 1/n. Samozrejme, potom limit Vyberme si teraz ako x n postupnosť so spoločným členom x n = -1/n, tiež smerujúca k nule. Preto neexistuje žiadny limit.

Príklad 3.6 . Dokážte, že neexistuje žiadny limit.

Riešenie.Nech x 1 , x 2 ,..., x n ,... je postupnosť, pre ktorú
. Ako sa postupnosť (f(x n)) = (sin x n) správa pre rôzne x n → ∞

Ak x n = p n, potom sin x n = sin p n = 0 pre všetky n a limit If
x n = 2 p n+ p /2, potom sin x n = sin(2 p n+ p /2) = sin p /2 = 1 pre všetkých n a teda limit. Takže neexistuje.

Widget na výpočet limitov online

V hornom okne namiesto sin(x)/x zadajte funkciu, ktorej limit chcete nájsť. V dolnom okne zadajte číslo, ku ktorému má smer x a kliknite na tlačidlo Výpočet, získajte požadovaný limit. A ak vo výsledkovom okne kliknete na Zobraziť kroky v pravom hornom rohu, dostanete podrobné riešenie.

Pravidlá pre zadávanie funkcií: sqrt(x) - druhá odmocnina, cbrt(x) - odmocnina, exp(x) - exponent, ln(x) - prirodzený logaritmus, sin(x) - sínus, cos(x) - kosínus, tan (x) - tangens, cot(x) - kotangens, arcsin(x) - arcsínus, arccos(x) - arkkozín, arctan(x) - arkustangens. Znaky: * násobenie, / delenie, ^ umocňovanie, namiesto toho nekonečno Nekonečno. Príklad: funkcia je zadaná ako sqrt(tan(x/2)).

Riešenie limity online funkcií. Nájdite limitnú hodnotu funkcie alebo funkčnej postupnosti v bode, vypočítajte konečný hodnota funkcie v nekonečne. určenie konvergencie číselného radu a oveľa viac sa dá urobiť vďaka našej online službe -. Umožňujeme vám rýchlo a presne nájsť limity funkcií online. Vy sami zadáte funkčnú premennú a hranicu, ku ktorej smeruje, a naša služba za vás vykoná všetky výpočty a poskytne presnú a jednoduchú odpoveď. A pre nájsť limit online môžete zadať číselné rady aj analytické funkcie obsahujúce konštanty v doslovnom vyjadrení. V tomto prípade nájdená limita funkcie bude obsahovať tieto konštanty ako konštantné argumenty vo výraze. Naša služba rieši akékoľvek zložité problémy pri hľadaní limity online, stačí uviesť funkciu a bod, v ktorom je potrebné počítať hraničná hodnota funkcie. Výpočet online limity, môžete použiť rôzne metódy a pravidlá na ich riešenie a zároveň kontrolovať výsledok získaný pomocou riešenie limitov online na stránke www.site, čo povedie k úspešnému dokončeniu úlohy - vyhnete sa vlastným chybám a administratívnym chybám. Alebo nám môžete úplne dôverovať a použiť náš výsledok vo svojej práci bez toho, aby ste vynaložili ďalšie úsilie a čas na samostatné vypočítanie limitu funkcie. Umožňujeme zadávanie limitných hodnôt, ako je nekonečno. Je potrebné zadať spoločný člen číselnej postupnosti a www.stránka vypočíta hodnotu limit online do plus alebo mínus nekonečna.

Jedným zo základných pojmov matematickej analýzy je limit funkcie A sekvenčný limit v bode a v nekonečne je dôležité vedieť správne riešiť limity. S našou službou to nebude ťažké. Je prijaté rozhodnutie limity online v priebehu niekoľkých sekúnd je odpoveď presná a úplná. Štúdium matematickej analýzy začína prechod na limit, limity sa používajú takmer vo všetkých oblastiach vyššej matematiky, preto je užitočné mať po ruke server online limitné riešenia, čo je stránka.

Funkčný limit- číslo a bude limitom nejakej premennej veličiny, ak sa v procese jej zmeny táto premenná veličina neobmedzene približuje a.

Alebo inými slovami, číslo A je hranica funkcie y = f(x) v bode x 0, ak sa pre ľubovoľnú postupnosť bodov z oblasti definície funkcie nerovná x 0, a ktorý konverguje k pointe x 0 (limit x n = x0), postupnosť zodpovedajúcich funkčných hodnôt konverguje k číslu A.

Graf funkcie, ktorej limita za predpokladu argumentu smerujúceho k nekonečnu sa rovná L:

Význam A je limit (limitná hodnota) funkcie f(x) v bode x 0 v prípade akejkoľvek postupnosti bodov , ktorá konverguje k x 0, ktorý však neobsahuje x 0 ako jeden z jeho prvkov (t. j. v prepichnutej blízkosti x 0), postupnosť funkčných hodnôt konverguje k A.

Limit Cauchyho funkcie.

Význam A bude limit funkcie f(x) v bode x 0 ak pre akékoľvek nezáporné číslo prijaté vopred ε nájde sa zodpovedajúce nezáporné číslo δ = δ(ε) tak, že pre každý argument X, splnenie podmienky 0 < | x - x0 | < δ , nerovnosť bude uspokojená | f(x)A |< ε .

Bude to veľmi jednoduché, ak pochopíte podstatu limitu a základné pravidlá na jeho nájdenie. Aká je hranica funkcie f (X) pri X usilovať sa o a rovná sa A, sa píše takto:

Navyše hodnota, ku ktorej premenná smeruje X, môže byť nielen číslo, ale aj nekonečno (∞), niekedy +∞ alebo -∞, alebo nemusí existovať žiadna hranica.

Aby ste pochopili ako nájsť limity funkcie, najlepšie je pozrieť si príklady riešení.

Je potrebné nájsť limity funkcie f (x) = 1/X na:

X→ 2, X→ 0, X→ ∞.

Poďme nájsť riešenie prvého limitu. Ak to chcete urobiť, môžete jednoducho nahradiť Xčíslo, ku ktorému má tendenciu, t.j. 2, dostaneme:

Nájdite druhú hranicu funkcie. Tu namiesto toho nahraďte čistú 0 X je to nemožné, pretože Nemôžete deliť 0. Ale môžeme vziať hodnoty blízke nule, napríklad 0,01; 0,001; 0,0001; 0,00001 a tak ďalej a hodnotu funkcie f (X) zvýši sa: 100; 1000; 10 000; 100 000 a tak ďalej. Dá sa teda pochopiť, že keď X→ 0 hodnota funkcie, ktorá je pod medzným znamienkom sa bude zvyšovať neobmedzene, t.j. usilovať sa o nekonečno. Čo znamená:

Čo sa týka tretieho limitu. Rovnakú situáciu ako v predchádzajúcom prípade nie je možné nahradiť ∞ vo svojej najčistejšej forme. Musíme zvážiť prípad neobmedzeného zvýšenia X. Nahrádzame 1000 po jednom; 10 000; 100 000 a tak ďalej, máme hodnotu funkcie f (x) = 1/X bude klesať: 0,001; 0,0001; 0,00001; a tak ďalej, sklon k nule. Preto:

Je potrebné vypočítať limitu funkcie

Keď začneme riešiť druhý príklad, vidíme neistotu. Odtiaľto nájdeme najvyšší stupeň čitateľa a menovateľa - to je x 3, vyberieme ho zo zátvoriek v čitateli a menovateli a potom ho zredukujeme o:

Odpoveď

Prvý krok v nájsť túto hranicu, namiesto toho nahraďte hodnotu 1 X, čo má za následok neistotu. Aby sme to vyriešili, rozložme čitateľa na faktorizáciu a urobme to pomocou metódy hľadania koreňov kvadratickej rovnice x 2 + 2x - 3:

D = 22 - 4*1*(-3) = 4 +12 = 16→ √ D=√16 = 4

x 1,2 = (-2±4)/2→ xi = -3;x 2= 1.

Čitateľ teda bude:

Odpoveď

Ide o definovanie jeho konkrétnej hodnoty alebo určitej oblasti, kam funkcia spadá, ktorá je limitovaná.

Ak chcete vyriešiť limity, postupujte podľa pravidiel:

Po pochopení podstaty a hlavného pravidlá riešenia limitu, získate základnú predstavu o tom, ako ich vyriešiť.