Jaké je 1 znamení, že trojúhelníky se rovnají? První znak rovnosti trojúhelníků: formulace a důkaz (7. stupeň). Jednoduché pravdy o trojúhelníkech

Věta 3.1 (trojúhelník znamení rovnosti na dvou stranách a úhel mezi nimi).Pokud dvě strany a roh mezi nimi jednoho trojúhelníku jsou stejné, v tomto pořadí, dvěma stranám a úhel mezi nimi jiného trojúhelníku, pak jsou takové trojúhelníky shodné.

Důkaz. Nechť trojúhelníky ABC a A 1 B 1 C 1 A = A 1, AB = A 1 B 1, AC = A 1 C 1 (obr. 44). Pojďme to dokázat trojúhelníky jsou rovny.

Nechť A 1 B 2 C 2 je trojúhelník rovný trojúhelníku ABC, s vrcholem B 2 na paprsku A 1 B 1 a vrcholem C 2 ve stejné polorovině vzhledem k přímce A 1 B 1, kde leží vrchol C 1 ( Obr. 45, a).

Protože A 1 B 1 = A 1 B 2, pak se vrchol B 2 shoduje s vrcholem B 1 (obr. 45.6). Protože B 1 A 1 C 1 = B 2 A 1 C 2, pak se paprsek A 1 C 2 shoduje s paprskem A 1 C 1 (obr. 45, c). Protože A 1 C 1 = A 1 C 2, pak se vrchol C 2 shoduje s vrcholem C 1 (obr. 45, d).

Takže trojúhelník A 1 B 1 C 1 se shoduje s trojúhelníkem A 1 B 2 C 2, což znamená, že se rovná trojúhelníku ABC. Věta byla prokázána.

Problém (1). Segmenty AB a CD se protínají v bodě O, který je středem každého z nich. Jaká je délka segmentu BD, je-li segment AC = 10 m?

Řešení. Trojúhelníky AOC a BOD jsou si rovny podle prvního znaménka trojúhelníková kongruence(obr. 46).

Jejich úhly AOC a BOD jsou stejné jako vertikální a OA=OB a OC=OD, protože bod O je středem segmentů AB a CD. Z rovnosti trojúhelníků AOC a BOD vyplývá, že jejich strany AC a BD jsou stejné. A protože podle podmínek úlohy AC = 10 m, pak BD = 10 m.

A. V. Pogorelov, Geometrie pro ročníky 7-11, Učebnice pro vzdělávací instituce

Shrnutí lekce

"První známka rovnosti trojúhelníků"

(lekce č. 1, ročník 7, podle učebnice L.S. Atanasyan)

Cíle lekce:

Vzdělávací:

Zavést pojem věta a důkaz věty;

Dokažte první znak rovnosti trojúhelníků;

Naučte se řešit úlohy pomocí prvního znaku rovnosti trojúhelníků.

Vývojový:

Rozvíjet schopnost porovnávat, shrnout poznatky, hodnotit vliv podmínek na výsledek;

Rozvíjet logické myšlení žáků.

Vzdělávací:

Rozvinout schopnost analyzovat data, vyvozovat logické důsledky z daných předpokladů a schopnost vyvozovat závěry;

Rozvíjet schopnost koncentrace a soustředění.

Metodický cíl: vyzkoušet si to nový přístup k formulaci věty, zjistit, zda studenti zachytí okamžik, kdy se podmínky stanou dostatečnými.

Typ lekce: kombinovaná.

Vybavení: počítač, plátno, projektor, prezentace, pravítko, trojúhelník,

barevné pastelky.

Během vyučování

Organizace času: (2 minuty)

V předchozí lekci jsme začali studovat kapitolu „Trojúhelníky“. Zjistili jsme, které dva obrazce, konkrétně dva trojúhelníky, se nazývají rovné. Dnes zjistíme, zda je možné stanovit rovnost dvou obrazců bez skutečného překrývání jednoho na druhého, ale porovnáním pouze některých prvků těchto obrazců, zejména jak porovnávat trojúhelníky.

Opakování probrané látky: ( 6 minut)

Zopakujme si látku z předchozí lekce.

Teoretický průzkum na následující otázky:

vysvětlit, jaká postava se nazývá trojúhelník;

nakreslit trojúhelník a ukázat jeho strany, vrcholy a úhly;

jaký je obvod trojúhelníku?

Které trojúhelníky se nazývají shodné?

Každý student dostane obálku obsahující 6-7 papírových trojúhelníků; Studenti jsou požádáni, aby mezi nimi našli sobě rovné.

Po dokončení hledání se zeptejte jednoho ze studentů, jak našel tento pár. Žák řekne, jak položil jeden trojúhelník na druhý.

Splnění praktického úkolu s následným ústním testem:

č. 1: Na tabuli (nebo diapozitivu) jsou nakresleny ∆DEK, ∆MNP.

Obrázek 1

Pojmenujte úhly:

a) ∆DEK sousedící se stranou EK;

b) ∆MNP sousedící se stranou MN.

Pojmenujte úhel:

a) ∆DEK, uzavřené mezi stranami DE a DK;

b) ∆MNP, uzavřená mezi stranami NP a RM.

Mezi kterými stranami:

a) ∆DEK svírá úhel K;

b) ∆MNP je součástí úhlu N?

Obrázek 2

Volám žáka k tabuli, on svou odpověď doprovází ukázkou na výkresech a psaní na tabuli.

3. Učení nového materiálu: ( 16 minut)

Chcete-li stanovit rovnost dvou trojúhelníků, musíte je zkombinovat nebo zkontrolovat rovnost odpovídajících stran a odpovídajících úhlů. Šest rovností! Někdy ale není možné zkombinovat nebo zkontrolovat všech šest rovností. Ano, to není nutné, ukázalo se, že stačí nainstalovat pouze některé z nich. Naším cílem je určit, které z těchto šesti rovností jsou skutečně nezbytné.

Takže máme problém.

Pojďme to vyřešit.

Obrázek 3

Ukazuje se, že tvrzení „Pokud se dvě strany a úhel mezi nimi jednoho trojúhelníku rovnají dvěma stranám a úhel mezi nimi jiného trojúhelníku, pak jsou takové trojúhelníky shodné“ je pravdivé. Toto tvrzení se nazývá „První znamení, že trojúhelníky jsou stejné“.

A v matematice každý výrok, jehož platnost je stanovena uvažováním, nazývá teorém, a samotná úvaha se nazývá důkaz věty.

Jaké věty už známe?

Vlastnictví sousední rohy a vlastnost vertikálních úhlů.

Proč se věta o rovnosti trojúhelníků nazývá kritérium?

Podepsat ( podle V. Dahla) je znakem, rozdílem, vším, proč něco uznávají. Když vidíte mrazivý vzor na okně, můžete říci, aniž byste opustili svůj domov, že je venku zima. Chcete-li zjistit, zda je číslo 7859467 dělitelné 9, není nutné provádět dělení: můžete použít test dělitelnosti.

Znak umožňuje stanovit rovnost dvou trojúhelníků, aniž by se jeden z nich ve skutečnosti překrýval na druhý, ale porovnáním pouze některých prvků trojúhelníků.

Každá věta se skládá z podmínky a závěru. Jak rozumíte tomu, co může znamenat fráze „podmínka věty“ a co může znamenat „závěr věty“?

Podmínkou jsou již známá fakta, která jsou ve větě probrána, a závěrem je to, co je potřeba dokázat.

Zvýrazněte podmínku věty „První kritérium pro rovnost trojúhelníků“.

Jestliže se dvě strany a úhel mezi nimi jednoho trojúhelníku rovnají dvěma stranám a úhlu mezi nimi jiného trojúhelníku.

Zvýrazněte závěr věty.

Pak jsou takové trojúhelníky shodné.

Pojďme tedy dokázat první známku rovnosti trojúhelníků:

Nyní se podívejme na další otázku. Nejprve si však pozorně poslechněte formulaci: Jestliže se dvě strany a úhel jednoho trojúhelníku rovnají dvěma stranám a úhlu jiného trojúhelníku, pak jsou takové trojúhelníky shodné. Myslíte si, že je toto tvrzení pravdivé?

Uvažujme ∆ABC a ∆ADC.

Obrázek 4

Strana AB trojúhelníku ABC se rovná straně AD trojúhelníku ADC, strana AC je společná a strana C je společná. Ale trojúhelníky nejsou stejné. Takže podmínka výroku je splněna, ale závěr nikoliv. To znamená, že tvrzení není pravdivé. Prosím zaplať Speciální pozornost, na to, že podmínka „mezi nimi“ je nutná!

4. Upevňování nového materiálu: (10 min)

Podívejme se, jak lze větu použít k řešení problémů.

Ústní řešení úloh pomocí předem připravených výkresů na zadní straně desky nebo na diapozitivu.

№2:

K vyřešení každého problému zavolám žáka k tabuli, kde se k řešení vyjádří, přičemž uvedené prvky ukáže ve výkresu. Zbytek studentů poslouchá, opraví a případně doplní odpověď.

Pozornost studentů zaměřuji na povinný obsah odkazu „trojúhelníky jsou stejné na dvou stranách a úhel mezi nimi“, a nikoli na formální „trojúhelníky se rovnají na prvním znaménku“, zjišťuji, zda všichni řešení pochopili a pokud vyvstanou otázky, odpovídám na ně sám.

Pokud problém vyžaduje, abyste dokázali, že dva trojúhelníky jsou shodné, co byste měli použít: definici nebo větu?

Samozřejmě, je to teorém. Podle definice musíte kombinovat trojúhelníky a podle věty musíte zkontrolovat tři rovnosti.

Na Obr. AB = AC, 1 = 2.

a) Dokažte, že trojúhelníky ABD a ACD jsou shodné;

b) najděte BD a AB, pokud AC = 15 cm, DC = 5 cm.

Dáno: AB = AC, 1 = 2,

AC=15 cm, DC=5 cm.

Dokázat:

∆АВD = ∆АСD.

Najít: ВD, АВ.

Důkaz: Před napsáním řešení na tabuli požádám žáky, aby problém řešili ústně. Jeden student komentujedůkaz. Dalším je zjištění délek segmentů. A pakZapíšeme řešení problému: Jsem na tabuli, studenti jsou v sešitech.

Možné řešení zadání:

Důkaz:

Uvažujme ∆АВD a ∆АСD.

AB = AC (podle konvence)

АD - společná strana ∆АВD = ∆АСD (podle dvou

1 = 2 (konvenční) strany a úhel mezi nimi)

Slovní komentář: trojúhelníky ABD a ACD jsou stejné na dvou stranách a úhel mezi nimi, první znak rovnosti trojúhelníků, který říká: „Pokud se dvě strany a úhel mezi nimi jednoho trojúhelníku rovnají dvěma stranám a úhlu mezi nimi jiného trojúhelníku, pak jsou takové trojúhelníky stejné."

ВD = DC = 5 cm, AB = AC = 15 cm (jako odpovídající prvky stejných trojúhelníků).

Odpověď: ВD = 5 cm, AB = 15 cm.

Zjišťuji, zda se během řešení objevily nějaké otázky.

5. Shrnutí lekce:(4 min)

Takže zopakujme:

Které trojúhelníky se nazývají rovné?

Jak se nazývá teorém?

Co se nazývá důkaz věty?

Jakou větu jsme dnes dokázali? Formulujte to.

Proč se věta nazývá znak?

Studenti odpovídají na otázky.

Práci v hodině hodnotím s komentáři.

6. Domácí práce: ( 2 minuty)

P 15. Otázky 3-4 s. 49-50. č. 93, 95.

č. 93. Segmenty AE a DC se protínají v bodě B, který je středem každého z nich. A) Dokažte, že trojúhelníky ABC a EBD jsou shodné; b) najděte úhly A a C trojúhelníku ABC, je-li v trojúhelníku BDE D = 470, E = 420.

č. 95. Na Obr. BC = AD, 1 = 2, a) Dokažte, že trojúhelníky ABC a CDA jsou shodné; b) Najděte AB a BC, pokud AD = 17 cm, DC = 14 cm.

Bibliografie:

Atanasyan L.S., Butuzov V.F., atd. Geometrie 7-9 ročníků. Učebnice pro ročníky 7-9 střední škola. - M.: Vzdělávání, 2006.

Atanasyan L.S., Butuzov V.F. a další Studium geometrie v 7.-9. Směrnice do učebnice. - M.: Vzdělávání, 2000.

Kovaleva G.I., Mazurová N.I. Testy pro proudovou a obecnou kontrolu. Nakladatelství "Učitel" 2008. .

Amelkin V.V., Rabcevič T.I. Školní geometrie ve výkresech a vzorcích. 2008.

V tomto článku vám řekneme, jak formulovat a dokázat první znak rovnosti trojúhelníků který se koná v 7. třídě.

Formulace prvního znaku rovnosti trojúhelníků

"Pokud se dvě strany a úhel mezi nimi jednoho trojúhelníku rovna dvěma stranám a úhel mezi nimi jiného trojúhelníku, pak jsou tyto trojúhelníky shodné."

Krátce se tomu říká rovnost "na dvou stranách a úhel mezi nimi."

Než se pohneme dál, je třeba si připomenout, co se nazývá trojúhelník a v takovém případě lze říci, že dva trojúhelníky jsou si rovny.

Co je trojúhelník a kdy jsou považovány za rovné?

Trojúhelník je geometrický obrazec tří úseček spojujících tři body (za předpokladu, že neleží na stejné přímce. Tyto body jsou uvažovány vrcholy trojúhelník. A segmenty, které je spojují, jsou strany).

Obrázek 1 ukazuje trojúhelník ABC. Který má tři vrcholy (A, B a C). A strany jsou AB, AC a BC.

Obrázek 1

Trojúhelníky jsou považovány za stejné, když jsou všechny jejich strany a úhly navzájem stejné (v případě, že jsou stejné pouze úhly a strany jsou úměrné, trojúhelníky se nazývají podobný). Je tedy zřejmé, že stejné trojúhelníky mohou být na sebe navrstveny - a budou se zcela shodovat.

Důkaz prvního znaku rovnosti trojúhelníků

Vzhledem k tomu:

Dva trojúhelníky: ABC a DEF (obrázek 2).

Obrázek 2

Podle podmínek věty jsou dvě dvojice úseček těchto trojúhelníků navzájem stejné (AC = FD a CB = EF). Úhly mezi segmenty jsou také stejné (tj. ∠ACV = ∠EFD).

Dokázatže trojúhelník ABC se rovná trojúhelníku DEF.

Důkaz:

Vzhledem k tomu, že existuje rovnost úhlů (∠ACB = ∠EFD), lze trojúhelníky poskládat na sebe tak, aby vrchol C splýval s vrcholem F.
V tomto případě budou segmenty CA a CB překrývat segmenty FE a FD.
A protože úsečky dvou trojúhelníků jsou si navzájem rovny (AC = FD a CB = EF podle podmínky), bude úsečka AB také splývat se stranou ED.
To zase povede ke kombinaci vrcholů A a D, B a E.
Trojúhelníčky tedy zcela zapadnou, což znamená, že jsou stejné.

Věta byla prokázána.

1) na dvou stranách a úhel mezi nimi

Důkaz:

Nechť trojúhelníky ABC a A 1 B 1 C 1 mají úhel A roven úhlu A 1, AB roven A 1 B 1, AC rovný A 1 C 1. Dokažme, že trojúhelníky jsou shodné.

Vložme trojúhelník ABC (nebo k němu symetricky) na trojúhelník A 1 B 1 C 1 tak, aby úhel A byl srovnaný s úhlem A 1 . Protože AB=A 1 B 1 a AC=A 1 C 1, pak B se bude shodovat s B 1 a C se bude shodovat s C 1. To znamená, že trojúhelník A 1 B 1 C 1 se shoduje s trojúhelníkem ABC, a proto je rovno trojúhelníku ABC.

Věta byla prokázána.

2) podél bočních a přilehlých rohů

Důkaz:

Nechť ABC a A 1 B 1 C 1 jsou dva trojúhelníky, ve kterých se AB rovná A 1 B 1, úhel A se rovná úhlu A 1 a úhel B se rovná úhlu B 1. Dokažme, že jsou si rovni.

Vložme trojúhelník ABC (nebo k němu symetricky) na trojúhelník A 1 B 1 C 1 tak, že AB se shoduje s A 1 B 1. Protože ∠BAC =∠B 1 A 1 C 1 a ∠ABC=∠A 1 B 1 C 1, bude paprsek AC splývat s A 1 C 1 a BC se budou shodovat s B 1 C 1. Z toho vyplývá, že vrchol C se shoduje s C 1. To znamená, že trojúhelník A 1 B 1 C 1 se shoduje s trojúhelníkem ABC, a proto je roven trojúhelníku ABC.

Věta byla prokázána.

3) na třech stranách

důkaz:

Uvažujme trojúhelníky ABC a A l B l C 1, ve kterých AB = A 1 B 1, BC = B l C 1 CA = C 1 A 1. Dokažme, že ΔАВС =ΔA 1 B 1 C 1.

Aplikujme trojúhelník ABC (nebo k němu symetricky) k trojúhelníku A 1 B 1 C 1 tak, že vrchol A je zarovnán s vrcholem A 1 , vrchol B je zarovnán s vrcholem B 1 a vrcholy C a C 1 jsou na opačných stranách přímky A 1 B 1 . Uvažujme 3 případy:

1) Paprsek C 1 C prochází uvnitř úhlu A 1 C 1 B 1. Protože jsou podle podmínek věty strany AC a A 1 C 1, BC a B 1 C 1 stejné, pak jsou trojúhelníky A 1 C 1 C a B 1 C 1 C rovnoramenné. Podle věty o vlastnosti úhlů rovnoramenného trojúhelníku ∠1 = ∠2, ∠3 = ∠4, tedy ∠ACB=∠A 1 C 1 B 1 .

2) Paprsek C 1 C se shoduje s jednou ze stran tohoto úhlu. A leží na CC 1. AC=A 1 C 1, BC=B 1 C 1, C 1 BC - rovnoramenné, ∠ACB=∠A 1 C 1 B 1.

3) Paprsek C 1 C prochází mimo úhel A 1 C 1 B 1. AC=A 1 C 1, BC=B 1 C 1, což znamená ∠1 = ∠2, ∠1+∠3 = ∠2+∠4, ∠ACB=∠A 1 C 1 B 1.

Takže AC=A1C1, BC=B1C1, ∠C=∠C1. Proto jsou trojúhelníky ABC a A 1 B 1 C 1 stejné
první kritérium pro rovnost trojúhelníků.

Věta byla prokázána.

2. Rozdělení segmentu na n stejných částí.

Nakreslete paprsek skrz A, položte na něj n stejných segmentů. Nakreslete přímku přes B a A n a rovnoběžné čáry k ní přes body A 1 - A n -1. Označme jejich průsečíky s AB. Získáme n segmentů, které jsou stejné podle Thalesovy věty.

Thalesova věta. Pokud je několik stejných segmentů rozloženo za sebou na jedné ze dvou čar a jejich konce protínající druhou čáru jsou nakresleny rovnoběžné čáry, odříznou stejné segmenty na druhé čáře.

Důkaz. AB = CD

1. Nakreslete přímky přes body A a C rovnoběžné s druhou stranou úhlu. Dostaneme dva rovnoběžníky AB 2 B 1 A 1 a CD 2 D 1 C 1. Podle vlastnosti rovnoběžníku: AB 2 = A 1 B 1 a CD 2 = C 1 D 1.

2. ΔABB 2 = ΔCDD 2 ABB 2 CDD 2 BAB 2 DCD 2 a jsou si rovny na základě druhého kritéria pro rovnost trojúhelníků:
AB = CD podle věty,
jako odpovídající, vzniklé v průsečíku rovnoběžné přímky BB 1 a DD 1 BD.

3. Podobně se ukáže, že každý z úhlů je roven úhlu s vrcholem v průsečíku sečen. AB 2 = CD 2 jako odpovídající prvky ve shodných trojúhelníkech.

4. A 1 B 1 = AB 2 = CD 2 = C 1 D 1

Při řešení geometrických úloh je užitečné řídit se takovým algoritmem. Při čtení podmínek problému je to nutné

Udělejte nákres. Výkres by měl co nejvíce odpovídat podmínkám problému, jeho hlavním úkolem je tedy pomoci najít řešení
Vložte všechna data z výpisu problému na výkres
Zapište všechny geometrické pojmy, které se v úloze vyskytují
Pamatujte si všechny věty, které se vztahují k těmto pojmům
Nakreslete na výkres všechny vztahy mezi prvky geometrického útvaru, které z těchto vět vyplývají

Pokud například úloha obsahuje slova osy úhlu trojúhelníku, musíte si zapamatovat definici a vlastnosti osy a ve výkresu označit stejné nebo proporcionální segmenty a úhly.

V tomto článku najdete základní vlastnosti trojúhelníku, které potřebujete znát pro úspěšné řešení problémů.

TROJÚHELNÍK.

Oblast trojúhelníku.

1. ,

zde - libovolná strana trojúhelníku, - výška snížená na tuto stranu.

2. ,

zde a jsou libovolné strany trojúhelníku a je to úhel mezi těmito stranami:

3. Heronův vzorec:

Zde jsou délky stran trojúhelníku, je půlobvod trojúhelníku,

4. ,

zde je půlobvod trojúhelníku a poloměr vepsané kružnice.

Nechť jsou délky tečných segmentů.

Potom lze Heronův vzorec napsat takto:

6. ,

zde - délky stran trojúhelníku, - poloměr kružnice opsané.

Vezmeme-li bod na straně trojúhelníku, který dělí tuto stranu v poměru m:n, pak úsečka spojující tento bod s vrcholem opačného úhlu rozdělí trojúhelník na dva trojúhelníky, jejichž plochy jsou v poměru m: n:

Poměr ploch podobných trojúhelníků se rovná druhé mocnině koeficientu podobnosti.

Medián trojúhelníku

Jedná se o segment spojující vrchol trojúhelníku se středem protější strany.

Mediány trojúhelníku protínají v jednom bodě a jsou rozděleny průsečíkem v poměru 2:1, počítáno od vrcholu.

Průsečík střednic pravidelného trojúhelníku rozděluje střednici na dva segmenty, z nichž menší se rovná poloměru kružnice vepsané a větší z nich se rovná poloměru kružnice opsané.

Poloměr kružnice opsané je dvojnásobkem poloměru kružnice vepsané: R=2r

Střední délka libovolný trojúhelník

zde - medián nakreslený na stranu - délky stran trojúhelníku.

Osa trojúhelníku

Toto je úsečka libovolného úhlu trojúhelníku spojující vrchol tohoto úhlu s opačnou stranou.

Osa trojúhelníku rozděluje stranu na segmenty úměrné sousedním stranám:

Osy trojúhelníku protínají v jednom bodě, který je středem vepsané kružnice.

Všechny body osy úhlu jsou stejně vzdálené od stran úhlu.

Výška trojúhelníku

Jedná se o kolmý segment spadlý z vrcholu trojúhelníku na opačnou stranu nebo jeho pokračování. V tupoúhlém trojúhelníku leží výška nakreslená z vrcholu ostrého úhlu mimo trojúhelník.

Výšky trojúhelníku se protínají v jednom bodě, který je tzv ortocentrum trojúhelníku.

Chcete-li zjistit výšku trojúhelníku natažené na stranu, potřebujete nějaké přístupným způsobem najděte jeho oblast a poté použijte vzorec:

Střed kružnice opsané trojúhelníku, leží v průsečíku odvěsnic nakreslených ke stranám trojúhelníku.

Poloměr obvodu trojúhelníku lze nalézt pomocí následujících vzorců:

Zde jsou délky stran trojúhelníku a je to plocha trojúhelníku.

kde je délka strany trojúhelníku a opačný úhel. (Tento vzorec vyplývá ze sinusové věty.)

Trojúhelníková nerovnost

Každá strana trojúhelníku je menší než součet a větší než rozdíl ostatních dvou.

Součet délek libovolných dvou stran je vždy větší než délka třetí strany:

Naproti větší straně leží větší úhel; Naproti většímu úhlu leží větší strana:

Pokud , tak naopak.

Věta o sinech:

Strany trojúhelníku jsou úměrné sinusům opačných úhlů:

Kosinová věta:

Druhá mocnina strany trojúhelníku se rovná součtu čtverců ostatních dvou stran bez dvojnásobku součinu těchto stran kosinusem úhlu mezi nimi:

Pravoúhlý trojuhelník

- Jedná se o trojúhelník, jehož jeden z úhlů je 90°.

Součet ostrých úhlů pravoúhlého trojúhelníku je 90°.

Přepona je strana, která leží proti úhlu 90°. Přepona je nejdelší strana.

Pythagorova věta:

druhá mocnina přepony se rovná součtu čtverců nohou:

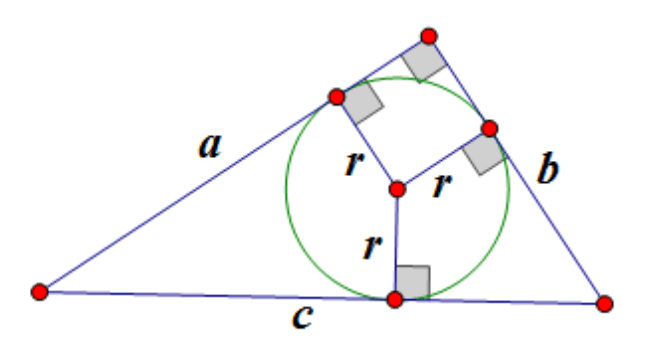
Poloměr kružnice vepsané do pravoúhlého trojúhelníku je roven

zde je poloměr vepsané kružnice, - nohy, - přepona:

Střed kružnice opsané pravoúhlého trojúhelníku leží uprostřed přepony:

Medián pravoúhlého trojúhelníku nakresleného na přeponu, se rovná polovině přepony.

Definice sinus, kosinus, tangens a kotangens pravoúhlého trojúhelníku Koukni se

Poměr prvků v pravoúhlém trojúhelníku:

Druhá mocnina výšky pravoúhlého trojúhelníku vedeného z vrcholu pravého úhlu se rovná součinu průmětů nohou na přeponu:

Druhá mocnina nohy se rovná součinu přepony a průmětu nohy na přeponu:

Noha ležící naproti rohu rovná polovině přepony:

Rovnoramenný trojúhelník.

Osa rovnoramenného trojúhelníku nakresleného k základně je medián a nadmořská výška.

V rovnoramenném trojúhelníku jsou základní úhly stejné.

Vrcholový úhel.

A - strany,

A - úhly na základně.

Výška, osa a medián.

Pozornost! Výška, osa a medián nakreslené na stranu se neshodují.

Pravidelný trojúhelník

(nebo rovnostranný trojúhelník ) je trojúhelník, jehož všechny strany a úhly jsou si navzájem stejné.

Plocha pravidelného trojúhelníku rovná

kde je délka strany trojúhelníku.

Střed kruhu vepsaného do pravidelného trojúhelníku, se shoduje se středem kružnice opsané pravidelnému trojúhelníku a leží v průsečíku střednic.

Průsečík střednic pravidelného trojúhelníku dělí střednici na dva segmenty, z nichž menší se rovná poloměru kružnice vepsané a větší z nich se rovná poloměru kružnice opsané.

Je-li jeden z úhlů rovnoramenného trojúhelníku 60°, pak je trojúhelník pravidelný.

Střední čára trojúhelníku

Jedná se o segment spojující středy dvou stran.

Na obrázku DE je střední čára trojúhelníku ABC.

Prostřední čára trojúhelníku je rovnoběžná se třetí stranou a rovná se jeho polovině: DE||AC, AC=2DE

Vnější úhel trojúhelníku

Toto je úhel sousedící s jakýmkoli úhlem trojúhelníku.

Vnější úhel trojúhelníku je roven součtu dvou úhlů, které s ním nesousedí.

Goniometrické funkce vnějšího úhlu:

Značky rovnosti trojúhelníků:

1 . Pokud se dvě strany a úhel mezi nimi jednoho trojúhelníku rovnají dvěma stranám a úhlu mezi nimi jiného trojúhelníku, pak jsou takové trojúhelníky shodné.

2 . Pokud se strana a dva sousední úhly jednoho trojúhelníku rovnají jedné straně a dvěma sousedním úhlům jiného trojúhelníku, pak jsou takové trojúhelníky shodné.

3 Pokud se tři strany jednoho trojúhelníku rovnají třem stranám jiného trojúhelníku, pak jsou takové trojúhelníky shodné.

Důležité: protože v pravoúhlém trojúhelníku jsou dva úhly zjevně stejné, pak pro rovnost dvou pravoúhlých trojúhelníků vyžaduje se rovnost pouze dvou prvků: dvou stran nebo strany a ostrého úhlu.

Známky podobnosti trojúhelníků:

1 . Pokud jsou dvě strany jednoho trojúhelníku úměrné dvěma stranám jiného trojúhelníku a úhly mezi těmito stranami jsou stejné, pak jsou tyto trojúhelníky podobné.

2 . Pokud jsou tři strany jednoho trojúhelníku úměrné třem stranám jiného trojúhelníku, pak jsou trojúhelníky podobné.

3 . Pokud se dva úhly jednoho trojúhelníku rovnají dvěma úhlům jiného trojúhelníku, pak jsou trojúhelníky podobné.

Důležité: V podobných trojúhelníkech leží podobné strany v opačných stejných úhlech.

Menelaova věta

Nechť čára protíná trojúhelník, a je bodem jeho průsečíku se stranou , je bodem jeho průsečíku se stranou , a je bodem jeho průsečíku s pokračováním strany . Pak